В статье дается краткое введение в парный трейдинг, включая концепцию, базовую математику, алгоритм стратегии, разработку торгового робота, оценку тестов на обратное тестирование и перенаправление, а также обсуждение будущих проблем. В качестве практического примера робот будет торговать на криптовалютах.
 Концепция
Концепция
Торговля парами - это нейтральная к рынку торговая стратегия, в которой используется длинная позиция с короткой позицией в паре сильно совмещенных активов.
Прибыль стратегии получается из разницы в изменении цены между двумя инструментами, а не из направления каждого движения. Следовательно, прибыль может быть получена, если длинная позиция поднимается больше, чем короткая, или короткая позиция опускается больше, чем длинная (в идеальной ситуации длинная позиция поднимается и короткая позиция падает, но это не является обязательным требованием для получение прибыли). Для парных трейдеров возможно получение прибыли в различных рыночных условиях, включая периоды, когда рынок идет вверх, вниз или в боковом тренде, а также в периоды низкой или высокой волатильности.
Коинтеграция против корреляции
В количественной торговле мы обычно работаем с нестационарными временными рядами. Часто люди считают коррелированными два актива, когда эти активы совмещаются, но этот термин является математически неверным в этом контексте. Корреляция Пирсона определяется только для стационарных переменных. Как видим, в этой формуле используются ожидаемые значения и стандартные отклонения, но эти значения меняются со временем в нестационарных процессах.
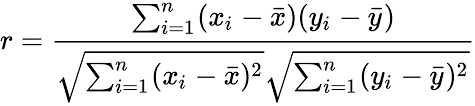
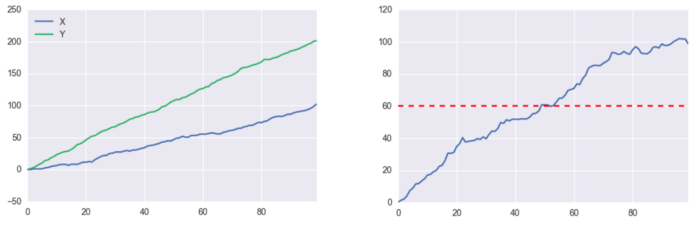
Для этих процессов мы можем определить коинтеграцию. Коинтеграция относится к некоторой стационарной линейной комбинации нескольких нестационарных временных рядов.
На этом рисунке показаны два процесса (X и Y) и их распространение.
Это пример корреляции без коинтеграции.
Этот пример наоборот (коинтеграция без корреляции)
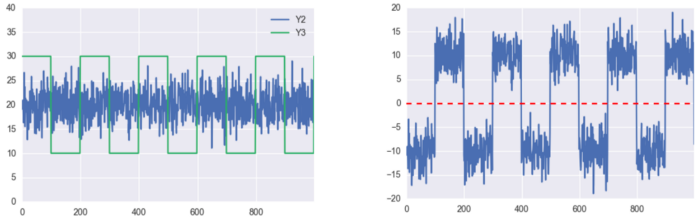
Коинтеграция без корреляции
Для перехода к следующей главе мы должны знать, как обнаружить коинтеграцию.
Три основных метода тестирования для коинтеграции:
1. Двухэтапный метод Энгла – Грейнджера
Если xt и yt нестационарны и коинтегрированы, то их линейная комбинация должна быть стационарной. Другими словами:
yt − βxt = ut, где ut стационарно.
Если бы мы знали ut, мы могли бы просто проверить его на стационарность с помощью чего-то вроде теста Дики-Фуллера, теста Филлипса-Перрона и сделать это. Но поскольку мы не знаем ut, мы должны сначала оценить это, обычно используя обычные наименьшие квадраты, а затем запустить наш тест на стационарность для оцененного ряда ut.
2. Тест Йохансена
Тест Йохансена - это тест на коинтеграцию, который допускает более одного отношения коинтеграции, в отличие от метода Энгла-Грейнджера, но этот тест имеет асимптотические свойства, то есть большие выборки. Если размер выборки слишком мал, результаты не будут надежными, и следует использовать авторегрессивную распределенную задержку (ARDL).
3. Тест коинтеграции Филлипса – Оусисиса
Peter C. B. Phillips и Sam Ouliaris (1990) показали, что основанные на остатках тесты единичного корня, применяемые к оцененным остаткам коинтеграции, не имеют обычных распределений Дики-Фуллера при нулевой гипотезе отсутствия коинтеграции. Из-за феномена ложной регрессии при нулевой гипотезе распределение этих тестов имеет асимптотическое распределение, которое зависит от (1) количества членов детерминированного тренда и (2) количества переменных, с которыми тестируется совместная интеграция. Эти распределения известны как распределения Филлипса – Ouliaris, и критические значения были сведены в таблицу. В конечных выборках лучшей альтернативой использованию этих асимптотических критических значений является генерация критических значений из моделирования.
Источник: Википедия
Давайте напишем небольшой анализ для этой проблемы. Прежде всего, загрузим данные из Bitfinex для нескольких криптовалют (с 2018–01–01 по 2018–05–31). Следующим шагом является построение графика криптовалюты. Наконец, выполняем проверку коинтеграции для всех пар активов.
Производительность криптовалюты
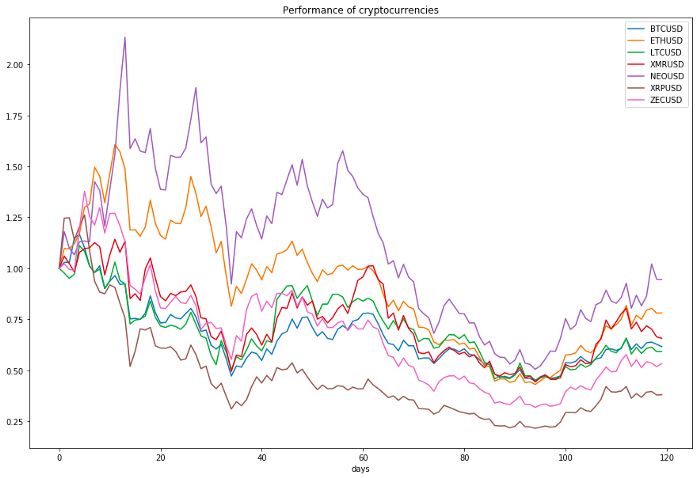
Производительность криптовалют (с 2018–01–01 по 2018–05–31)
Нулевая гипотеза состоит в том, что нет коинтеграции, альтернативная гипотеза состоит в том, что существуют коинтегрирующие отношения. Если значение p мало, ниже критического размера, мы можем отвергнуть гипотезу об отсутствии коинтегрирующих отношений.
Мы можем заключить, что некоторые из этих пар объединены и могут быть выбраны для следующего исследования.
Торговая стратегия
В торговле парами нет единого подхода, как рассчитать спред и торговать этим. Некоторые из подходов используют линейную регрессию и остатки в качестве спреда.Мы будем использовать следующий алгоритм.
Алгоритмическая стратегия содержит следующие шаги:
1. Определите коинтегрированные пары одним из методов, описанных выше (например, Энгл-Грейнджер). Этот шаг должен выполняться периодически для получения пары (или нескольких пар), которые будут использоваться на следующих шагах.
2. Получите историю цен активов по длине N. Рассчитайте доходность каждого актива (например, A и B) в паре.
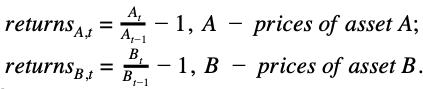
3. Рассчитайте разницу между доходами

4. Рассчитайте z-показатель, z-показатель - это число стандартных отклонений от среднего значения, которым является точка данных.
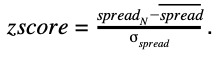
Эта картина иллюстрирует Z-счет
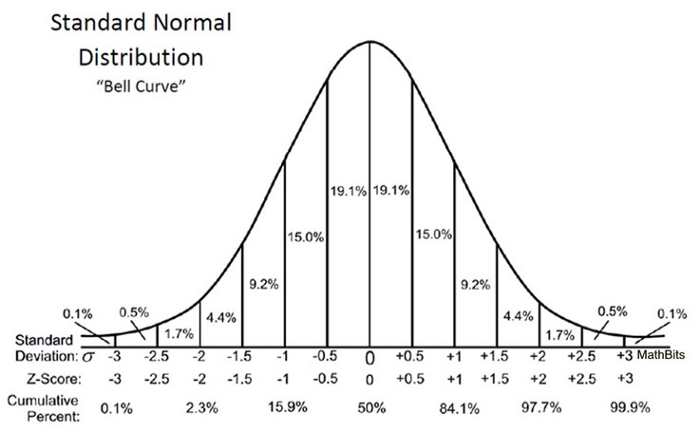
5. Проверьте правило ввода позиции:
Откройте длинную позицию для A (50% капитала) и короткую позицию для B (50% капитала), если это условие верно:
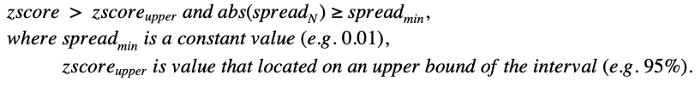
Откройте короткую позицию для A и длинную позицию для B, если это условие верно:
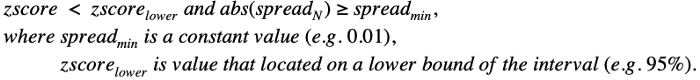
Давайте закодируем этот алгоритм с использованием фреймворка Catalyst. Если вам интересно краткое введение в Catalyst, то пишите в комментариях и увидите. Информацию о функциях initialize, handle_data, analysis и run_algorithm тоже озвучим.
Стандартный подход использует разделение train \ test split, но у нас также есть период тестирования коинтеграции в нашем случае. Эти периоды не должны пересекаться. Поэтому мы имеем
Период тестирования коинтеграции - 5 месяцев (с 2018–01–01 по 2018–05–31)
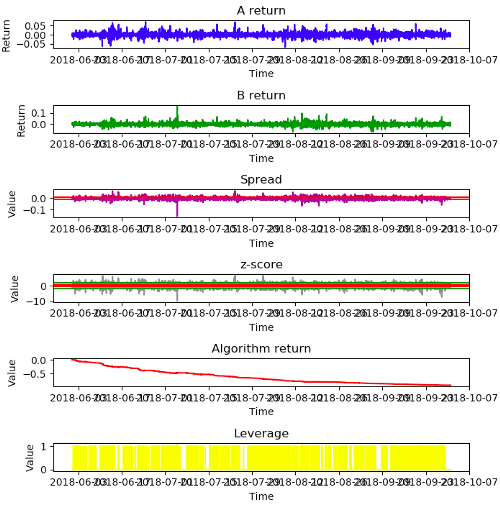
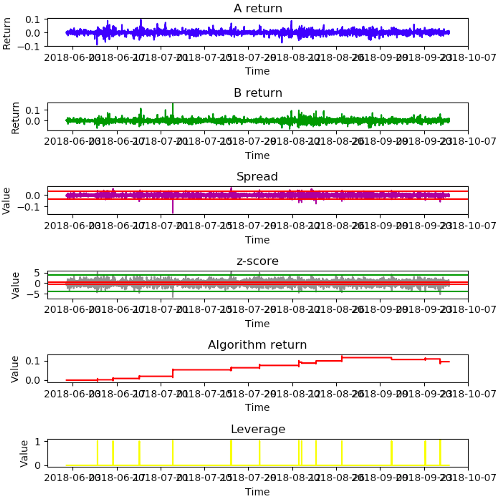
Период тестирования - 4 месяца (с 2018–06–01 по 2018–9–30)
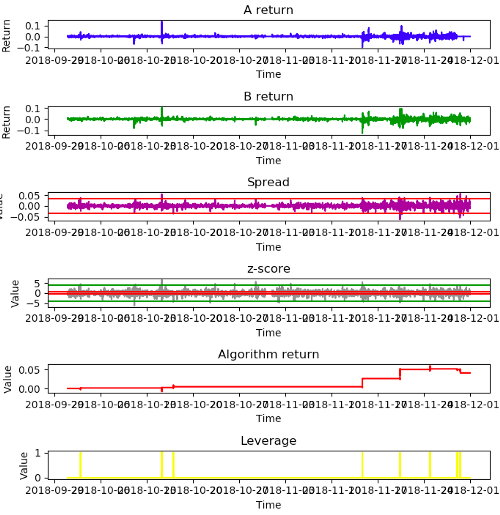
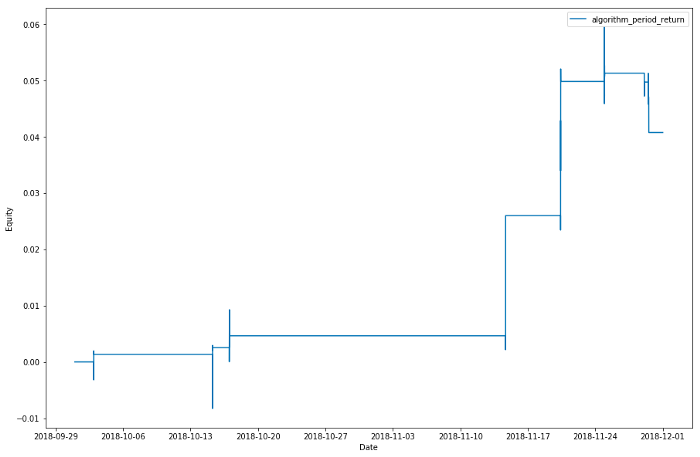
Период пересылки - 2 месяца (с 2018–10–1 по 2018–11–30)
Прежде всего, мы должны проверить алгоритм. Давайте запустим этот скрипт, используя пару XMR / USD и NEO / USD, отключив комиссионные расходы и отключив модель проскальзывания.
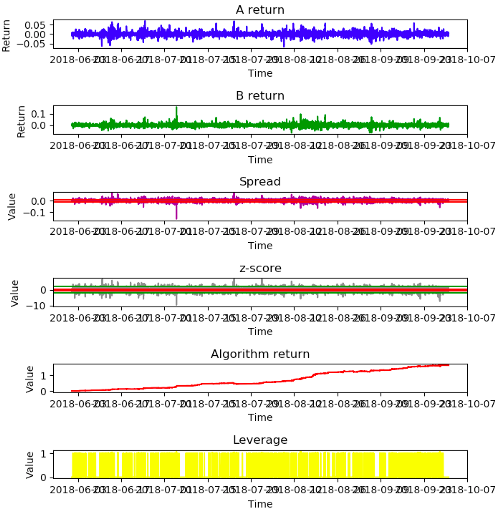
Как видим, кривая возврата алгоритма довольно хорошая. Похоже, как это должно работать (очень высокий коэффициент Сортино и доходность составляет 164% за 4 месяца). Консоль выводит производительность:
Общий доход: 1.6415993234216582
Сортино, 30,971434947620118
Максимальная просадка: -0.05125165292172551
Продолжение ниже...

Торговля парами - это нейтральная к рынку торговая стратегия, в которой используется длинная позиция с короткой позицией в паре сильно совмещенных активов.
Прибыль стратегии получается из разницы в изменении цены между двумя инструментами, а не из направления каждого движения. Следовательно, прибыль может быть получена, если длинная позиция поднимается больше, чем короткая, или короткая позиция опускается больше, чем длинная (в идеальной ситуации длинная позиция поднимается и короткая позиция падает, но это не является обязательным требованием для получение прибыли). Для парных трейдеров возможно получение прибыли в различных рыночных условиях, включая периоды, когда рынок идет вверх, вниз или в боковом тренде, а также в периоды низкой или высокой волатильности.
Коинтеграция против корреляции
В количественной торговле мы обычно работаем с нестационарными временными рядами. Часто люди считают коррелированными два актива, когда эти активы совмещаются, но этот термин является математически неверным в этом контексте. Корреляция Пирсона определяется только для стационарных переменных. Как видим, в этой формуле используются ожидаемые значения и стандартные отклонения, но эти значения меняются со временем в нестационарных процессах.
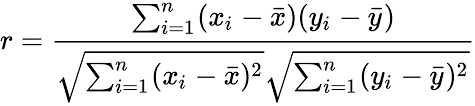
Для этих процессов мы можем определить коинтеграцию. Коинтеграция относится к некоторой стационарной линейной комбинации нескольких нестационарных временных рядов.
На этом рисунке показаны два процесса (X и Y) и их распространение.
Это пример корреляции без коинтеграции.

Этот пример наоборот (коинтеграция без корреляции)

Коинтеграция без корреляции
Для перехода к следующей главе мы должны знать, как обнаружить коинтеграцию.
Три основных метода тестирования для коинтеграции:
1. Двухэтапный метод Энгла – Грейнджера
Если xt и yt нестационарны и коинтегрированы, то их линейная комбинация должна быть стационарной. Другими словами:
yt − βxt = ut, где ut стационарно.
Если бы мы знали ut, мы могли бы просто проверить его на стационарность с помощью чего-то вроде теста Дики-Фуллера, теста Филлипса-Перрона и сделать это. Но поскольку мы не знаем ut, мы должны сначала оценить это, обычно используя обычные наименьшие квадраты, а затем запустить наш тест на стационарность для оцененного ряда ut.
2. Тест Йохансена
Тест Йохансена - это тест на коинтеграцию, который допускает более одного отношения коинтеграции, в отличие от метода Энгла-Грейнджера, но этот тест имеет асимптотические свойства, то есть большие выборки. Если размер выборки слишком мал, результаты не будут надежными, и следует использовать авторегрессивную распределенную задержку (ARDL).
3. Тест коинтеграции Филлипса – Оусисиса
Peter C. B. Phillips и Sam Ouliaris (1990) показали, что основанные на остатках тесты единичного корня, применяемые к оцененным остаткам коинтеграции, не имеют обычных распределений Дики-Фуллера при нулевой гипотезе отсутствия коинтеграции. Из-за феномена ложной регрессии при нулевой гипотезе распределение этих тестов имеет асимптотическое распределение, которое зависит от (1) количества членов детерминированного тренда и (2) количества переменных, с которыми тестируется совместная интеграция. Эти распределения известны как распределения Филлипса – Ouliaris, и критические значения были сведены в таблицу. В конечных выборках лучшей альтернативой использованию этих асимптотических критических значений является генерация критических значений из моделирования.
Источник: Википедия
Давайте напишем небольшой анализ для этой проблемы. Прежде всего, загрузим данные из Bitfinex для нескольких криптовалют (с 2018–01–01 по 2018–05–31). Следующим шагом является построение графика криптовалюты. Наконец, выполняем проверку коинтеграции для всех пар активов.
Код:
import quandl
import pandas as pd
from matplotlib import pyplot as plt
import requests
import statsmodels.tsa.stattools as ts
from statsmodels.tsa.vector_ar.vecm import coint_johansen
def get_bitfinex_asset(asset, ts_ms_start, ts_ms_end):
url = 'https://api.bitfinex.com/v2/candles/trade:1D:t' + asset + '/hist'
params = { 'start': ts_ms_start, 'end': ts_ms_end, 'sort': 1}
r = requests.get(url, params = params)
data = r.json()
return pd.DataFrame(data)[2]
start_date = 1514768400000 # 1 January 2018, 00:00:00
end_date = 1527811199000 # 31 May 2018, 23:59:59
assets = ['BTCUSD', 'ETHUSD', 'LTCUSD', 'XMRUSD', 'NEOUSD', 'XRPUSD', 'ZECUSD']
crypto_prices = pd.DataFrame()
for a in assets:
print('Downloading ' + a)
crypto_prices[a] = get_bitfinex_asset(asset = a, ts_ms_start = start_date, ts_ms_end = end_date)
crypto_prices.head()
# Normalize prices by first value
norm_prices = crypto_prices.divide(crypto_prices.iloc[0])
plt.figure(figsize = (15, 10))
plt.plot(norm_prices)
plt.xlabel('days')
plt.title('Performance of cryptocurrencies')
plt.legend(assets)
plt.show()
for a1 in crypto_prices.columns:
for a2 in crypto_prices.columns:
if a1 != a2:
test_result = ts.coint(crypto_prices[a1], crypto_prices[a2])
print(a1 + ' and ' + a2 + ': p-value = ' + str(test_result[1]))
Производительность криптовалют (с 2018–01–01 по 2018–05–31)
Нулевая гипотеза состоит в том, что нет коинтеграции, альтернативная гипотеза состоит в том, что существуют коинтегрирующие отношения. Если значение p мало, ниже критического размера, мы можем отвергнуть гипотезу об отсутствии коинтегрирующих отношений.
Код:
BTCUSD and ETHUSD: p-value = 0.06576979804268955
BTCUSD and LTCUSD: p-value = 0.07347140678450967
BTCUSD and XMRUSD: p-value = 0.021570889424181703
BTCUSD and NEOUSD: p-value = 0.10239483419041967
BTCUSD and XRPUSD: p-value = 0.00900122457399106
BTCUSD and ZECUSD: p-value = 0.16378128244807538
ETHUSD and BTCUSD: p-value = 0.31796015423321283
ETHUSD and LTCUSD: p-value = 0.609075825185015
ETHUSD and XMRUSD: p-value = 0.17284643088428048
ETHUSD and NEOUSD: p-value = 0.12876967722061067
ETHUSD and XRPUSD: p-value = 0.8353724771161415
ETHUSD and ZECUSD: p-value = 0.008516903095807236
LTCUSD and BTCUSD: p-value = 0.32518789859253106
LTCUSD and ETHUSD: p-value = 0.16681383335780392
LTCUSD and XMRUSD: p-value = 0.1740000549876129
LTCUSD and NEOUSD: p-value = 0.12495042850291554
LTCUSD and XRPUSD: p-value = 0.34798612459501926
LTCUSD and ZECUSD: p-value = 0.2208460047208785
XMRUSD and BTCUSD: p-value = 0.03688944104750657
XMRUSD and ETHUSD: p-value = 0.06850494599390901
XMRUSD and LTCUSD: p-value = 0.18455770053115805
XMRUSD and NEOUSD: p-value = 0.15900072498514983
XMRUSD and XRPUSD: p-value = 0.10535218181116313
XMRUSD and ZECUSD: p-value = 0.08687381831452784
NEOUSD and BTCUSD: p-value = 0.6594245361268345
NEOUSD and ETHUSD: p-value = 0.10139553534891843
NEOUSD and LTCUSD: p-value = 0.5917795242081397
NEOUSD and XMRUSD: p-value = 0.31992922945348756
NEOUSD and XRPUSD: p-value = 0.702811523154505
NEOUSD and ZECUSD: p-value = 0.19217634013579027
XRPUSD and BTCUSD: p-value = 0.38260792567369073
XRPUSD and ETHUSD: p-value = 0.8809574619059632
XRPUSD and LTCUSD: p-value = 0.41282018472796755
XRPUSD and XMRUSD: p-value = 0.2295414704744081
XRPUSD and NEOUSD: p-value = 0.061273680287838465
XRPUSD and ZECUSD: p-value = 0.6935781798945656
ZECUSD and BTCUSD: p-value = 0.36470825863289646
ZECUSD and ETHUSD: p-value = 0.06280072073557352
ZECUSD and LTCUSD: p-value = 0.4757981312526575
ZECUSD and XMRUSD: p-value = 0.1008622413530807
ZECUSD and NEOUSD: p-value = 0.19230331197251305
ZECUSD and XRPUSD: p-value = 0.893919204241542Торговая стратегия
В торговле парами нет единого подхода, как рассчитать спред и торговать этим. Некоторые из подходов используют линейную регрессию и остатки в качестве спреда.Мы будем использовать следующий алгоритм.
Алгоритмическая стратегия содержит следующие шаги:
1. Определите коинтегрированные пары одним из методов, описанных выше (например, Энгл-Грейнджер). Этот шаг должен выполняться периодически для получения пары (или нескольких пар), которые будут использоваться на следующих шагах.
2. Получите историю цен активов по длине N. Рассчитайте доходность каждого актива (например, A и B) в паре.
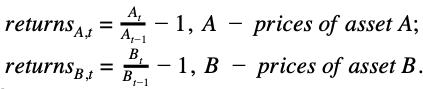
3. Рассчитайте разницу между доходами

4. Рассчитайте z-показатель, z-показатель - это число стандартных отклонений от среднего значения, которым является точка данных.
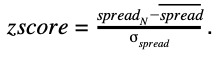
Эта картина иллюстрирует Z-счет

5. Проверьте правило ввода позиции:
Откройте длинную позицию для A (50% капитала) и короткую позицию для B (50% капитала), если это условие верно:
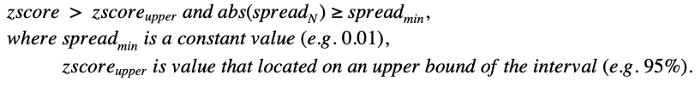
Откройте короткую позицию для A и длинную позицию для B, если это условие верно:
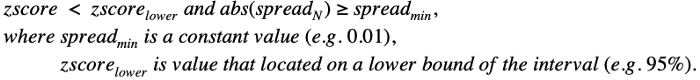
Давайте закодируем этот алгоритм с использованием фреймворка Catalyst. Если вам интересно краткое введение в Catalyst, то пишите в комментариях и увидите. Информацию о функциях initialize, handle_data, analysis и run_algorithm тоже озвучим.
Код:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.stats as st
from catalyst import run_algorithm
from catalyst.api import (record, symbol, order_target_percent, date_rules, time_rules, get_datetime)
def initialize(context):
context.A = symbol('xmr_usd')
context.B = symbol('neo_usd')
context.leverage = 1.0 # 1.0 - no leverage
context.n_modelling = 144 # number of lookback bars for modelling
context.tf = str(30) + "T" # how many minutes in a timeframe; 1 - to get minute data (often errors happen); 60 - to get hourly data
context.z_signal_in = st.norm.ppf(1 - 0.05 / 2) # z-score threshold to open an order
context.z_signal_out = st.norm.ppf(1 - 0.60 / 2) # z-score threshold to close an order
context.min_spread = 0.01 # threshold for minimal allowed spread
context.set_commission(maker = 0.000, taker = 0.000)
context.set_slippage(slippage = 0.0000)
def handle_data(context, data):
current_time = get_datetime().time()
# Get data
A = data.history(context.A,
'price',
bar_count = context.n_modelling,
frequency = context.tf,
)
B = data.history(context.B,
'price',
bar_count = context.n_modelling,
frequency = context.tf,
)
# Calc returns and spread
A_return = A.pct_change()
B_return = B.pct_change()
spread = A_return - B_return
zscore = (spread.iloc[-1] - spread.mean()) / spread.std()
# Close positions
if context.portfolio.positions[context.B].amount < 0 and zscore >= -context.z_signal_out:
order_target_percent(context.A, 0.0)
order_target_percent(context.B, 0.0)
if context.portfolio.positions[context.B].amount > 0 and zscore <= context.z_signal_out:
order_target_percent(context.A, 0.0)
order_target_percent(context.B, 0.0)
# Check minimal allowed spread value
if (abs(spread[-1]) >= context.min_spread):# and np.sign(A_return[-1] * B_return[-1]) < 0:
# Long and Short positions for assets
if context.portfolio.positions[context.B].amount == 0 and zscore > context.z_signal_in:
order_target_percent(context.A, -0.5 * context.leverage)
order_target_percent(context.B, 0.5 * context.leverage)
if context.portfolio.positions[context.B].amount == 0 and zscore < -context.z_signal_in:
order_target_percent(context.A, 0.5 * context.leverage)
order_target_percent(context.B, -0.5 * context.leverage)
record(
A_return = A_return[-1],
B_return = B_return[-1],
spread = spread[-1],
zscore = zscore
)
def analyze(context, perf):
# Summary output
print("Total return: " + str(perf.algorithm_period_return[-1]))
print("Sortino coef: " + str(perf.sortino[-1]))
print("Max drawdown: " + str(np.min(perf.max_drawdown)))
f = plt.figure(figsize = (7.2, 7.2))
# Plot 1st A group
ax1 = f.add_subplot(611)
ax1.plot(perf.A_return, 'blue')
ax1.set_title('A return')
ax1.set_xlabel('Time')
ax1.set_ylabel('Return')
# Plot 2nd public group
ax2 = f.add_subplot(612, sharex = ax1)
ax2.plot(perf.B_return, 'green')
ax2.set_title('B return')
ax2.set_xlabel('Time')
ax2.set_ylabel('Return')
# Plot spread
ax3 = f.add_subplot(613, sharex = ax1)
ax3.plot(perf.spread, 'darkmagenta')
ax3.axhline(context.min_spread, c = 'red')
ax3.axhline(-context.min_spread, c = 'red')
ax3.set_title('Spread')
ax3.set_xlabel('Time')
ax3.set_ylabel('Value')
# Plot z-score
ax4 = f.add_subplot(614, sharex = ax1)
ax4.plot(perf.zscore, 'grey')
ax4.axhline(context.z_signal_in, c = 'green')
ax4.axhline(-context.z_signal_in, c = 'green')
ax4.axhline(context.z_signal_out, c = 'red')
ax4.axhline(-context.z_signal_out, c = 'red')
ax4.set_title('z-score')
ax4.set_xlabel('Time')
ax4.set_ylabel('Value')
# Plot return
ax5 = f.add_subplot(615, sharex = ax1)
ax5.plot(perf.algorithm_period_return, 'red')
ax5.set_title('Algorithm return')
ax5.set_xlabel('Time')
ax5.set_ylabel('Value')
# Plot leverage
ax6 = f.add_subplot(616, sharex = ax1)
ax6.plot(perf.gross_leverage, 'yellow')
ax6.set_title('Leverage')
ax6.set_xlabel('Time')
ax6.set_ylabel('Value')
plt.tight_layout()
plt.show()
run_algorithm(
capital_base = 10000,
data_frequency = 'minute',
initialize = initialize,
handle_data = handle_data,
analyze = analyze,
exchange_name = 'bitfinex',
quote_currency = 'usd',
start = pd.to_datetime('2018-6-1', utc = True),
end = pd.to_datetime('2018-9-30', utc = True))Период тестирования коинтеграции - 5 месяцев (с 2018–01–01 по 2018–05–31)
Период тестирования - 4 месяца (с 2018–06–01 по 2018–9–30)
Период пересылки - 2 месяца (с 2018–10–1 по 2018–11–30)
Прежде всего, мы должны проверить алгоритм. Давайте запустим этот скрипт, используя пару XMR / USD и NEO / USD, отключив комиссионные расходы и отключив модель проскальзывания.

Как видим, кривая возврата алгоритма довольно хорошая. Похоже, как это должно работать (очень высокий коэффициент Сортино и доходность составляет 164% за 4 месяца). Консоль выводит производительность:
Общий доход: 1.6415993234216582
Сортино, 30,971434947620118
Максимальная просадка: -0.05125165292172551
Продолжение ниже...
Последнее редактирование модератором: